Understanding Absolute Returns, Annualized Returns and CAGR
You earn money and spend what is necessary to end up with something what we call savings. You go out and look for best investment products available to invest into, which you expect to fetch some decent returns for your portfolio. Ever wondered how much you can lose by haphazardly investing in products which base their return calculations on something else than you think of?
Stock trader would be beneficiary with return evaluation standards
Lack of this knowledge might end up investment in a substandard asset and hence it becomes important to understand two basic yet important investment statistics: annualized and absolute returns.
Absolute return: The absolute return is probably the simplest way of calculating returns wherein the original investment is subtracted from the total return. To calculate the percent return, this difference is divided by the original investment and multiplied by 100.
Absolute returns = [(Final Value – Principal)/ (Principal)]*100
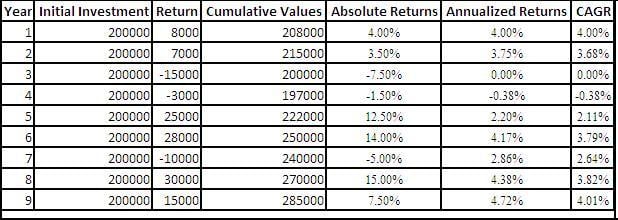
Let’s consider an example: You invested Rs 200000/- in year 1 which surged to Rs 285000/- in year 9.
According to the above mentioned formula the absolute return comes out to be 42.50%.
Calculation: – [(285000-200000)/200000]*100
Annualized return:
Simply put, it is the absolute returns divided by number of years the investment was held by the investor. In above example, it come out to be 42.50/9= 4.72%
Compounded Annual Growth Rate:
CAGR (Compounded Annual Growth Rate): CAGR makes the return calculation far more efficient and is slightly complicated than absolute or annualized returns but provides a better measure of time adjusted returns. CAGR takes into account not only the return, but also how long it took to get that return. This implies that by using CAGR, one can easily calculate what your portfolio earned over and above the market returns.
CAGR = [(Final Value/principal) ^ (365/days)] – 1 or
CAGR = [(Final Value/principal) ^ 1/years] – 1
CAGR takes into account the compounding of interest values. It is calculated based on adding first year returns to the principal amount for calculation of next year’s returns and so on and so forth.
Considering the previous example again,
CAGR= [(285000/200000) ^ 1/9]-1
=4.01%
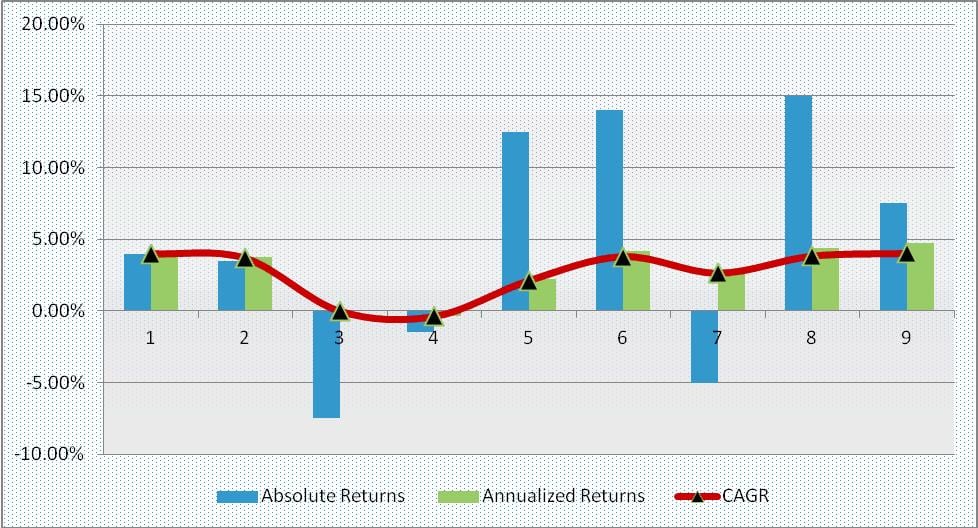
As is clear from the above example that absolute return showed a huge positive return whereas CAGR smoothed it out, removing noise from the calculation. However, the limitation CAGR has is that it doesn’t reflect investment risk i.e. volatility of returns. The overall investment may remain volatile during its tenure but CAGR gives one smoothed out value of return for the entire period. Absolute return faces a limitation that it doesn’t tell anything about the rate of return generated year on year.
The table given below shows all three types of return calculation for the example discussed above:
 Which return calculation to be used?
Which return calculation to be used?
Various return calculations are required so as to compare apples with apples and not with oranges. For comparing various funds, portfolios, benchmarking etc., different types of returns helps take an informed decision for investors. Absence of right evaluation standards might up in diversion from the financial goals.
Open Lowest Brokerage
Trading Account Now
[email-subscribers namefield=”NO” desc=”Subscribe now to get latest updates!” group=”Public”]













[…] Also Read : Return Evaluation Standards […]
Thats True. You need to plan both, your investment as well as returns.
We hope our articles add up more knowledge to it. Also, do not miss our next blog 🙂
Very useful to learn about return